😀 ORB-SLAM2 代码解读（三）：优化 2（详解 + g2o 使用）

0. 基本使用

0.1 构造 g2o 模型

首先构造 g2o 模型，包括选择线性方程求解器、矩阵求解器和下降算法；

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// 设置图模型创建优化器.
g2o::SparseOptimizer optimizer;
// 使用Cholmod中的线性方程求解器得到 linearSolver
g2o::BlockSolver_6_3::LinearSolverType * linearSolver;
linearSolver = new g2o::LinearSolverDense<g2o::BlockSolver_6_3::PoseMatrixType>();
// 再用稀疏矩阵块求解器 solver_ptr
g2o::BlockSolver_6_3 * solver_ptr = new g2o::BlockSolver_6_3(linearSolver);
// 选择梯度下降方法：L-M 算法 求解上面的 solver_ptr 得到 solver.
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
// 设置求解器.
optimizer.setAlgorithm(solver);
// 打开调试输出
optimizer.setVerbose( true );

0.2 g2o 类图

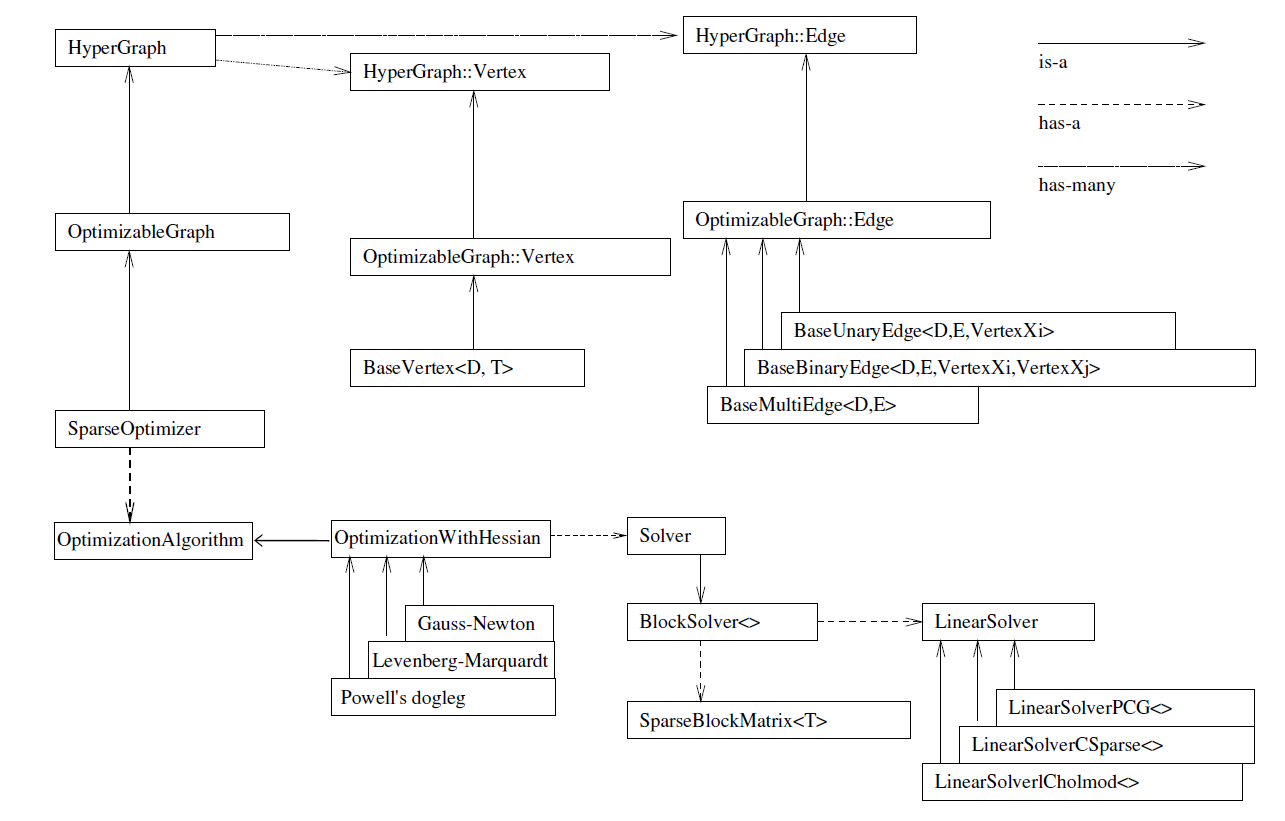
先给出前面初始化的代码再看类图吧，直接看图一脸懵，参考高翔的博客
上图中左侧的 SparseOptimizer 是第一步初始化的图模型，也是最终要维护的；
先看下半部分，对应前面的初始化代码，用于指定求解器和迭代算法，一个 SparseOptimizer 拥有一个 Optimization Algorithm ，其优化算法继承自 Gauss-Newton, Levernberg-Marquardt, Powell's dogleg 三者之一，不同的方法表现为最终的 H 矩阵构造不同；同时这个 Optimization Algorithm 拥有一个 Solver ，其包含两个部分：
- 一个是 SparseBlockMatrix ，用于计算稀疏的雅克比和海森矩阵；
- 另一个是构造线性方程求解器，可以从 PCG, CSparse, Choldmod 三者选则，用于计算迭代过程中最关键的一步 $$ H \Delta x = -b $$
然后看上半部分 SparseOptimizer 是一个 Optimizable Graph ，从而也是一个 Hyper Graph（超图），一个 SparseOptimizer 含有很多个顶点和很多个边；
- 顶点继承自 Base Vertex，也就是 OptimizableGraph::Vertex；
- 边继承自 OptimizableGraph::Edge，又分为 BaseUnaryEdge（单边）, BaseBinaryEdge（双边）或 BaseMultiEdge（多边）；
- 这些 Base Vertex 和 Base Edge 都是抽象的基类，而实际用的顶点和边，都是它们的派生类；
- 用 SparseOptimizer.addVertex() 和 SparseOptimizer.addEdge() 向一个图中添加顶点和边，最后调用 SparseOptimizer.optimize() 完成优化。

综上所述，在 g2o 中选择优化方法一共有三个步骤

步骤一： 选择线性方程 $H \Delta x = -b$ 的线性方程求解器，完全采用第三方的线性代数库，主要采用 Cholesky 分解和 PCG 迭代，具体可以选择的有
- Cholmod，CSparse （以上两者为比较著名的线性代数库），
- PCG （pre-conditioner is block Jacobi），
- Dense（dense Cholesky decomposition），
- 或者 ORB-SLAM中使用的Eigen（sparse Cholesky decoposition from Eigen）

步骤二： 块求解器 BlockSolver 构造线性方程求解器所需要的**矩阵块（H 和 b）**，需要用到边的雅克比 $$ H = J^{T}WJ, \quad b=J^{T}W\delta $$

需要指定优化变量的维度，常见的有以下几种，其中 6 表示待优化变量的维度， 3 表示误差项的维度，可以设置为动态的 BlockSolverX

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


// variable size solver
using BlockSolverX = BlockSolverPL<Eigen::Dynamic, Eigen::Dynamic>;

// solver for BA/3D SLAM
using BlockSolver_6_3 = BlockSolverPL<6, 3>;

// solver fo BA with scale
using BlockSolver_7_3 = BlockSolverPL<7, 3>;

// 2Dof landmarks 3Dof poses
using BlockSolver_3_2 = BlockSolverPL<3, 2>;

步骤三： 选择下降迭代策略，从 GN, LM, Doglog 中选择。

结合前面 0.1 节，总结一下 g2o 使用的流程

步骤一： 创建线性方程求解器，确定分解方法

1
2
3
4
5


// 每个误差项优化变量维度为3，误差值维度为1
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block;  
// 创建一个线性求解器 LinearSolver，采用 dense cholesky 分解法
Block::LinearSolverType* linearSolver 
    = new g2o::LinearSolverDense<Block::PoseMatrixType>(); 

要求解的增量方程为 $H \Delta x = -b$，通常想到的方法就是直接求逆 $\Delta x = -H^{-1}*b$，对于较小维度的 H 矩阵可以直接求逆，但当 H 维度较大时采用下面的方法进行求逆：
- LinearSolverCholmod：使用 sparse cholesky 分解法，继承自LinearSolverCCS；
- LinearSolverCSparse：使用 CSparse 法，继承自LinearSolverCCS；
- LinearSolverPCG ：使用preconditioned conjugate gradient 法，继承自 LinearSolver
- LinearSolverDense ：使用 dense cholesky 分解法，继承自 LinearSolver
- LinearSolverEigen：依赖项只有 eigen，使用 eigen 中 sparse Cholesky 求解，因此编译好后可以方便的在其他地方使用，性能和 CSparse 差不多，继承自 LinearSolver；

步骤二： 构造线性方程的矩阵块，并用上面定义的线性求解器初始化
1

Block* solver_ptr = new Block( linearSolver );
- BlockSolver 内部包含 LinearSolver，用上面定义的线性求解器 LinearSolver 来初始化，前面已经给定了优化变量的维度；

步骤三： 创建总求解器 solver，并从 GN, LM, DogLeg 中选一个，再用上述块求解器 BlockSolver 初始化

1

g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );

优化算法

1
2
3


g2o::OptimizationAlgorithmGaussNewton
g2o::OptimizationAlgorithmLevenberg 
g2o::OptimizationAlgorithmDogleg 

步骤四： 创建稀疏优化器（SparseOptimizer）

1
2
3


g2o::SparseOptimizer optimizer;     // 图模型
optimizer.setAlgorithm( solver );   // 用前面定义好的求解器作为求解方法：
optimizer.setVerbose( true );       // 打开调试输出

步骤五： 定义图的顶点和边，并添加到 SparseOptimizer 优化器中

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


// 创建一个顶点
CurveFittingVertex* v = new CurveFittingVertex(); 
// 初始化顶点的值
v->setEstimate( Eigen::Vector3d(0,0,0) );
// 设置顶点的编号
v->setId(0);
// 向图中添加顶点
optimizer.addVertex( v );
      
for ( int i=0; i<N; i++ )    // 往图中增加边
{
    // 创建一条边
    CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
    // 设置边的 id
    edge->setId(i);
    // 设置边连接的顶点
    edge->setVertex( 0, v );                
    // 设置观测数值
    edge->setMeasurement( y_data[i] );      
    // 设置信息矩阵：协方差矩阵之逆
    edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); 
    // 将边添加到图中
    optimizer.addEdge( edge );
}

步骤六： 设置优化参数，开始执行优化

1
2


optimizer.initializeOptimization();
optimizer.optimize(100); // 迭代次数

1. g2o 的顶点（Vertex）

1.1 顶点的格式

回到前面的类图上面的顶点部分的箭头，g2o 提供了一个比较通用的适合大多数情况的模板类 BaseVertex<D, T>（定义在 g2o/core/base_vertex.h 中），其继承自 OptimizableGraph::Vertex（定义在 g2o/core/optimizable_graph.h 中），OptimizableGraph 又继承自 HyperGraph::Vertex（定义在 g2o/core/hyper_graph.h 中），后两者都比较底层，一般使用第一个。

再来看看 BaseVertex<D, T> 类的模板参数 D，T
- D 是 int 类型，表示顶点 Vertex 的最小维度，比如 3D 空间中旋转是 3 维的，那么这里 D=3；
  - 在源码注释中说 D 并非是顶点（更确切的说是状态变量）的维度，而是其在流形空间（manifold）的最小表示
    1
    
    static const int Dimension = D; ///< dimension of the estimate (minimal) in the manifold space
- T 是待估计 Vertex 的数据类型，比如用四元数表达三维旋转的话，T 就是 Quaternion 类型
  1 2
  
  typedef T EstimateType; EstimateType _estimate;

g2o 提供的常用的顶点类型，若没有的类型可参考自己定义

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


VertexSE2 : public BaseVertex<3, SE2> //2D pose Vertex, (x,y,theta)
VertexSE3 : public BaseVertex<6, SE3Quat>
VertexSE3 : public BaseVertex<6, Isometry3>
VertexPointXY : public BaseVertex<2, Eigen::Vector2d>
VertexPointXYZ : public BaseVertex<3, Vector3>
VertexLine2D : public BaseVertex<2, Line2D>
VertexLine3D : public BaseVertex<4, Line3D>
VertexSegment2D : public BaseVertex<4, Vector4>
VertexCircle : public g2o::BaseVertex<3, Eigen::Vector3d>
VertexPlane : public BaseVertex<3, Plane3D>
VertexCam : public BaseVertex<6, SBACam>
VertexPosition3D : public g2o::BaseVertex<3, Eigen::Vector3d>
VertexPositionVelocity3D : public g2o::BaseVertex<6, Vector6d>
VertexOdomDifferentialParams: public BaseVertex <3, Vector3>
VertexCameraBAL : public BaseVertex<9, Eigen::VectorXd>
VertexSim3Expmap : public BaseVertex<7, Sim3>
VertexParams : public g2o::BaseVertex<3, Eigen::Vector3d>
VertexSE3Expmap : public BaseVertex<6, SE3Quat>
VertexBaseline : public BaseVertex<1, double>

顶点主要的成员函数（位于 g2o/core/base_vertex.h 中）

1
2


// 返回优化之后顶点的值.
const EstimateType& estimate() const { return _estimate;}

1.2 自定义顶点

自定义一个顶点需要重写以下函数
1 2 3 4

virtual bool read(std::istream& is); virtual bool write(std::ostream& os) const; virtual void setToOriginImpl(); virtual void oplusImpl(const number_t* update);
- read() 和 write() 读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅声明一下就可以了；
- setToOriginImpl() 是顶点重置函数，设置被优化变量的初始值；
- oplusImpl() 是顶点更新函数，主要用于优化过程中增量 $\Delta x$ 的计算；

自定义顶点类的格式

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25


class myVertex: public g2::BaseVertex<Dim, Type>
{
public:
  // 类成员变量如果是固定大小对象需要加上以下的宏定义
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  // 构造函数
  myVertex(){}
      
  // 读写函数
  virtual void read(std::istream& is) {}
  virtual void write(std::ostream& os) const {}

  // 重置函数
  virtual void setOriginImpl()
  {
      _estimate = Type();
  }
    
  // 更新函数
  virtual void oplusImpl(const double* update) override
  {
      _estimate += /*update*/;
  }
}

举例一： 以 SLAM 十四讲中曲线拟合的曲线模型顶点为例

定义顶点为 CurveFittingVertex，顶点维度为 3，类型为 Eigen::Vector3d；
初始值设为为 0, 0, 0；
更新函数中由于是向量直接加上更新量 _estimate += Eigen::Vector3d(update)；
读写函数留空。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
      
    // 重置
    virtual void setToOriginImpl() 
    {
        _estimate << 0,0,0;
    }
      
    // 更新
    virtual void oplusImpl( const double* update ) 
    {
        _estimate += Eigen::Vector3d(update);
    }
      
    // 存盘和读盘：留空
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
};

举例二： 以李代数表示的位姿作为顶点，位于 g2o/types/sba/types_six_dof_expmap.h 中

定义顶点类为 VertexSE3Expmap，优化变量是 6 自由度的李代数；
更新函数采用李代数的增量扰动更新

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


/**
 * \brief SE3 Vertex parameterized internally with a transformation matrix
 and externally with its exponential map
 */
class  VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  // 构造函数.
  VertexSE3Expmap();

  // 1. 读盘.
  bool read(std::istream& is);
  // 2. 写盘.
  bool write(std::ostream& os) const;

  // 3. 顶点重置函数，设定被优化变量的原始值
  virtual void setToOriginImpl() {
    _estimate = SE3Quat();
  }

  // 4. 顶点更新函数，增量更新
  virtual void oplusImpl(const double* update_)  {
    Eigen::Map<const Vector6d> update(update_);
    setEstimate(SE3Quat::exp(update)*estimate());
  }
};

举例三： 以三维向量表示的三维点作为顶点，位于 g2o/types/types_sba.h 中

定义顶点类为 VertexSBAPointXYZ，优化变量是 3 维度的 Vector3d 向量；
重置与更新函数类似于举例一中的形式，直接相加。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class VertexSBAPointXYZ : public BaseVertex<3, Vector3d>
{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW    
    VertexSBAPointXYZ();
    virtual bool read(std::istream& is);
    virtual bool write(std::ostream& os) const;

    virtual void setToOriginImpl() {
      _estimate.fill(0.);
    }

    virtual void oplusImpl(const double* update)
    {
      Eigen::Map<const Vector3d> v(update);
      _estimate += v;
    }
};

1.3 将顶点添加到图中

步骤：
- ① 创建顶点
- ② 设置初始值
- ③ 设置节点编号
- ④ 添加到优化器中

举例一：曲线拟合

1
2
3
4


CurveFittingVertex* v = new CurveFittingVertex();
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );

举例二：三维坐标点

1
2
3
4
5
6
7
8
9


int index = 1;
for ( const Point3f p:points_3d )   // landmarks
{
g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
point->setId ( index++ );
point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
point->setMarginalized ( true ); 
optimizer.addVertex ( point );
}

2. g2o 中的边

2.1 边的格式

还是回到前面的类图，关注右上角的边部分，我们一般使用的类是 BaseUnaryEdge，BaseBinaryEdge，BaseMultiEdge 分别表示一元边，两元边，多元边（位于 g2o/g2o/core/base_edge.h 中），类似于顶点，他们又继承自 OptimizableGraph::Edge （位于 g2o/g2o/core/optimizable_graph.h 中），hyper_graph::Edge（位于 g2o/g2o/core/hyper_graph.h 中）。
一元边表示只连接一个顶点，二元边表示连接两个顶点，多元边表示连接 3 个或以上顶点。

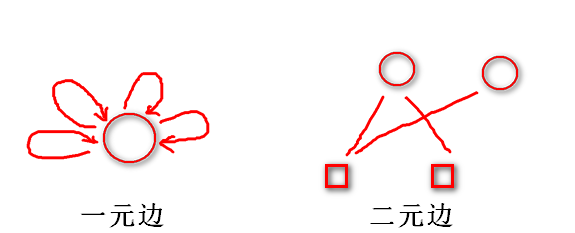
主要参数有：D, E, VertexXi, VertexXj
- D 是 int 型，表示测量值的维度；
- E 表示测量值的数据类型；
- VertexXi，VertexXj 分别表示不同顶点的类型。
- 举例：用边表示三维点投影到图像平面的重投影误差
  1
  
  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>
  - 首先顶点有两个是个，这是一个二元边；
  - 误差（测量值）的维度为 2，也就是像素坐标 u,v 的差值；
  - 误差（测量值）的数据类型为二维向量 Vector2D；
  - 两个顶点也就是优化变量分别是三维点 VertexSBAPointXYZ 和李群表示的相机位姿VertexSE3Expmap。

2.2 自定义边

自定义边需要重写以下成员函数
1 2 3 4

virtual bool read(std::istream& is); virtual bool write(std::ostream& os) const; virtual void computeError(); virtual void linearizeOplus();
- read() 和 write() 读盘、存盘函数，一般情况下不需要进行读/写操作的话，仅声明一下就可以了；
- computeError()：重要，计算当前顶点计算出的测量值与真实的测量值之间的误差；
- linearizeOplus()：重要，在当前顶点的值下，该误差对优化变量的偏导数，也就是 Jacobian。

除以上几个成员函数之外还有几个重要的成员变量和函数

1
2
3
4
5
6
7


_measurement：存储观测值
_error：存储computeError() 函数计算的误差
_vertices[]：存储顶点信息，比如二元边的话，_vertices[] 的大小为2，存储顺序和调用setVertex(int, vertex) 是设定的int 有关（0 或1）
setId(int)：来定义边的编号（决定了在H矩阵中的位置）
setMeasurement(type) 函数来定义观测值
setVertex(int, vertex) 来定义顶点
setInformation() 来定义协方差矩阵的逆

自定义边的格式：类似于定义顶点，但重点是 computeError()，linearizeOplus() 两个函数，也更复杂

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
{
      public:
      EIGEN_MAKE_ALIGNED_OPERATOR_NEW      
      myEdge(){}     
      virtual bool read(istream& in) {}
      virtual bool write(ostream& out) const {}  
        
      virtual void computeError() override
      {
          // ...
          _error = _measurement - Something;
      }      
        
      virtual void linearizeOplus() override
      {
          _jacobianOplusXi(pos, pos) = something;
          // ...         
          /*
          _jocobianOplusXj(pos, pos) = something;
          ...
          */
      }      
      private:
      // data
}

举例一：一元边。来源十四讲中的曲线拟合

定义误差边为 CurveFittingEdge，维度为 1，类型为 double，连接的顶点为 CurveFittingVertex；

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
      
    CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
      
    // 计算曲线模型误差
    void computeError()
    {
        const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
        const Eigen::Vector3d abc = v->estimate();
        _error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
    }
      
    virtual bool read( istream& in ) {}
    virtual bool write( ostream& out ) const {}
public:
    double _x;  // x 值， y 值为 _measurement
};

举例二：二元边。3D-2D点的PnP 问题，也就是最小化重投影误差问题，来源于 g2o/types/sba/types_six_dof_expmap.h

构造边为 EdgeProjectXYZ2UV，维度为 2，类型为 Vector2D，连接的两个顶点分别为三维点 VertexSBAPointXYZ 和李群表示的相机位姿 VertexSE3Expmap；

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


//继承了BaseBinaryEdge类，观测值是2维，类型Vector2D,顶点分别是三维点、李群位姿
class G2O_TYPES_SBA_API EdgeProjectXYZ2UV : public  BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
      
    //1. 构造函数初始化
    EdgeProjectXYZ2UV();
      
    //2. 计算误差
    void computeError()  
    {
      // 李群相机位姿 顶点 v1
      const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
      // 三维点 顶点 v2
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
      //相机参数
      const CameraParameters * cam
        = static_cast<const CameraParameters *>(parameter(0));
     //误差计算，测量值减去估计值，也就是重投影误差obs-cam
     //估计值计算方法是T*p,得到相机坐标系下坐标，然后在利用camera2pixel()函数得到像素坐标。
      Vector2D obs(_measurement);
      _error = obs-cam->cam_map(v1->estimate().map(v2->estimate()));
    }
      
    //3. 线性增量函数，也就是雅克比矩阵J的计算方法
    virtual void linearizeOplus();
      
    //4. 相机参数
    CameraParameters * _cam; 
    bool read(std::istream& is);
    bool write(std::ostream& os) const;
};

关于误差计算函数：误差 = 观测 - 投影
1

_error = obs - cam->cam_map(v1->estimate().map(v2->estimate()));
- 其中 obs 是观测值，当前帧中观察到的特征点的像素坐标；
- v1 是相机位姿，v2 是地图点坐标，cam 是相机参数；
- v1->estimate().map(v2->estimate()) 是利用相机位姿（外参）将地图点坐标从世界坐标系转换到相机坐标系；（.map 操作定义在 g2o/types/sim3/sim3.h 中）
- cam->cam_map(v1->estimate().map(v2->estimate())) 是利用相机内参将地图点从相机坐标系转换到图像坐标系。（cam_map 操作定义在 g2o/types/sba/types_six_dof_expmap.cpp 中）

关于雅克比矩阵的计算函数 linearizeOplus()：误差（观测相机方程）关于相机位姿和三维点的偏导数

上式分别对应下面代码中的 _jacobianOplusXj 和 _jacobianOplusXi（代码位于 g2o/g2o/types/sba/types_six_dof_expmap.cpp 中）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


  void EdgeProjectXYZ2UV::linearizeOplus() {
  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat T(vj->estimate());
  VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
  Vector3D xyz = vi->estimate();
  Vector3D xyz_trans = T.map(xyz);

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double z = xyz_trans[2];
  double z_2 = z*z;

  const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));

  Matrix<double,2,3,Eigen::ColMajor> tmp;
  tmp(0,0) = cam->focal_length;
  tmp(0,1) = 0;
  tmp(0,2) = -x/z*cam->focal_length;

  tmp(1,0) = 0;
  tmp(1,1) = cam->focal_length;
  tmp(1,2) = -y/z*cam->focal_length;

  _jacobianOplusXi =  -1./z * tmp * T.rotation().toRotationMatrix();

  _jacobianOplusXj(0,0) =  x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(0,1) = -(1+(x*x/z_2)) *cam->focal_length;
  _jacobianOplusXj(0,2) = y/z *cam->focal_length;
  _jacobianOplusXj(0,3) = -1./z *cam->focal_length;
  _jacobianOplusXj(0,4) = 0;
  _jacobianOplusXj(0,5) = x/z_2 *cam->focal_length;

  _jacobianOplusXj(1,0) = (1+y*y/z_2) *cam->focal_length;
  _jacobianOplusXj(1,1) = -x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(1,2) = -x/z *cam->focal_length;
  _jacobianOplusXj(1,3) = 0;
  _jacobianOplusXj(1,4) = -1./z *cam->focal_length;
  _jacobianOplusXj(1,5) = y/z_2 *cam->focal_length;
}

2.3 将边添加到图中

举例一：一元边。 以曲线拟合为例（slambook/ch6/g2o_curve_fitting/main.cpp）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


for ( int i=0; i<N; i++ )
{
    // 创建边
    CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );
      
    edge->setId(i);                         // 设置边的 id
    edge->setVertex( 0, v );                // 设置连接的顶点
    edge->setMeasurement( y_data[i] );      // 观测数值
      
    // 信息矩阵：协方差矩阵之逆
    edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); 
      
    // 将边添加到图中
    optimizer.addEdge( edge );
}

举例二：二元边。 位于 slambook/ch7/pose_estimation_3d2d.cpp 中

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


index = 1;
for ( const Point2f p:points_2d )
{
    // 创建边.
    g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
    // 设置边的 id
    edge->setId ( index );
    // 指定连接的顶点
    edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
    edge->setVertex ( 1, pose );
      
    // 设置观测值
    edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
      
    edge->setParameterId ( 0,0 );
      
    edge->setInformation ( Eigen::Matrix2d::Identity() );
      
    optimizer.addEdge ( edge );
    index++;
}

注意在 setVertex() 中设置顶点的 id 和类型时要与边的类中定义的相对应，比如定义边时 v1 表示相机位姿，id 为 1，v2 表示三维点，id 为0

1
2
3
4
5
6


class G2O_TYPES_SBA_API EdgeProjectXYZ2UV 
.....
 //李群相机位姿v1
const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
// 顶点v2
const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);

3. ORB-SLAM2 中的顶点

前一篇文章笔记提到在 ORB-SLAM2 中顶点有三个，SE(3) 相机位姿、地图点坐标、闭环检测时的 sim(3) 相机位姿；
- 在每帧的位姿优化 Optimizer::PoseOptimization() 函数中只将相机位姿作为顶点；
- 在 BA 优化 中将相机位姿和地图点两者作为顶点；
- 在闭环时将 sim(3) 相机位姿作为顶点。

3.1 相机位姿顶点

与前面自定义顶点的举例二中一样，即 g2o/types/types_six_dof_expmap.h 中 6 维李代数表示的 VertexSE3Expmap。

3.2 地图点坐标顶点

与前面自定义顶点的举例三中一样，即 g2o/types/types_sba.h 中三维向量表示的 VertexSBAPointXYZ。

3.3 闭环时的 sim3 相机位姿

与 6 维李代数表示的相机为了多了一个尺度因子

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54


// BRIEF 7 维 Sim3 表示的相机位姿.（用于闭环），增加了一个尺度 s.
  class VertexSim3Expmap : public BaseVertex<7, Sim3>
  {
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    VertexSim3Expmap();

    virtual bool read(std::istream& is);
    virtual bool write(std::ostream& os) const;

    // 重置函数，尺度因子 s 设置为 1.
    virtual void setToOriginImpl() {
      _estimate = Sim3();
    }

    // 顶点更新函数.
    virtual void oplusImpl(const double* update_)
    {
      Eigen::Map<Vector7d> update(const_cast<double*>(update_));

      if (_fix_scale)
        update[6] = 0;

      Sim3 s(update);
      setEstimate(s*estimate());
    }

    Vector2d _principle_point1, _principle_point2;
    Vector2d _focal_length1, _focal_length2;

    // 地图点投影到闭环帧的坐标？
    Vector2d cam_map1(const Vector2d & v) const
    {
      Vector2d res;
      res[0] = v[0]*_focal_length1[0] + _principle_point1[0];
      res[1] = v[1]*_focal_length1[1] + _principle_point1[1];
      return res;
    }

    // 地图点投影到当前帧的坐标？
    Vector2d cam_map2(const Vector2d & v) const
    {
      Vector2d res;
      res[0] = v[0]*_focal_length2[0] + _principle_point2[0];
      res[1] = v[1]*_focal_length2[1] + _principle_point2[1];
      return res;
    }

    bool _fix_scale;


  protected:
  };

4. ORB-SLAM2 中的边

4.1 位姿优化时的重投影误差

在 PoseOptimization() 仅优化相机位姿 时，重投影误差是一个一元边，顶点（优化变量）为相机的位姿。对应 g2o/types/types_six_dof_expmap.h 中定义的边 EdgeSE3ProjectXYZOnlyPose。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42


// BRIEF 一元边：重投影误差（仅用于优化相机位姿时）
class  EdgeSE3ProjectXYZOnlyPose: public  BaseUnaryEdge<2, Vector2d, VertexSE3Expmap>
{
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  EdgeSE3ProjectXYZOnlyPose(){}

  bool read(std::istream& is);

  bool write(std::ostream& os) const;

  // 误差计算函数.
  void computeError()  
  {
    // 李代数表示的相机位姿 v1（顶点）.
    const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[0]);

    // 观测值：特征点当前帧中的坐标.
    Vector2d obs(_measurement);

    // 重投影误差，.map() 是将地图点的世界坐标转换到相机坐标系，cam_project() 操作将其投影到当前帧.
    _error = obs-cam_project(v1->estimate().map(Xw));
  }

  // 检查地图点在相机坐标系中的深度是否为正.
  bool isDepthPositive() 
  {
    const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[0]);
    return (v1->estimate().map(Xw))(2)>0.0;
  }

  // 雅克比矩阵：重投影误差相对于相机位姿的一阶导.
  virtual void linearizeOplus();

  // 投影到当前帧.
  Vector2d cam_project(const Vector3d & trans_xyz) const;

  Vector3d Xw;  // 地图点的世界坐标.

  double fx, fy, cx, cy;  // 相机参数.
}; // 边：重投影误差（仅用于优化相机位姿时）.

其中 linearizeOplus() 函数构造雅克比矩阵，对应 g2o/types/types_six_dof_expmap.cpp 中的 void EdgeSE3ProjectXYZOnlyPose::linearizeOplus()

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


// BRIEF 优化相机位姿是重投影误差的雅克比矩阵（对相机位姿的偏导）
void EdgeSE3ProjectXYZOnlyPose::linearizeOplus() 
{
  // 顶点：相机位姿.
  VertexSE3Expmap * vi = static_cast<VertexSE3Expmap *>(_vertices[0]);
  // 地图点的相机坐标.
  Vector3d xyz_trans = vi->estimate().map(Xw);

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double invz = 1.0/xyz_trans[2];
  double invz_2 = invz*invz;

  _jacobianOplusXi(0,0) =  x*y*invz_2 *fx;
  _jacobianOplusXi(0,1) = -(1+(x*x*invz_2)) *fx;
  _jacobianOplusXi(0,2) = y*invz *fx;
  _jacobianOplusXi(0,3) = -invz *fx;
  _jacobianOplusXi(0,4) = 0;
  _jacobianOplusXi(0,5) = x*invz_2 *fx;

  _jacobianOplusXi(1,0) = (1+y*y*invz_2) *fy;
  _jacobianOplusXi(1,1) = -x*y*invz_2 *fy;
  _jacobianOplusXi(1,2) = -x*invz *fy;
  _jacobianOplusXi(1,3) = 0;
  _jacobianOplusXi(1,4) = -invz *fy;
  _jacobianOplusXi(1,5) = y*invz_2 *fy;
} // 优化相机位姿是重投影误差的雅克比矩阵.

4.2 BA 优化时的重投影误差

在 BA 优化时优化的量包括相机位姿和地图点坐标，重投影误差是一个二元边，连接的顶点为李代数表示的相机位姿和三维向量表示的地图点坐标。对应 g2o/types/types_six_dof_expmap.h 中定义的边 EdgeSE3ProjectXYZ，其定义格式与前面自定义边中举例二的二元边一样。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


// BRIEF 边：重投影误差（BA优化时）
class  EdgeSE3ProjectXYZ: public  BaseBinaryEdge<2, Vector2d, VertexSBAPointXYZ, VertexSE3Expmap>
{
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW

  EdgeSE3ProjectXYZ();

  bool read(std::istream& is);

  bool write(std::ostream& os) const;

  // 误差计算函数
  void computeError()  
  {
    // 顶点 v1：相机位姿，顶点的 id 为 1.
    const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
    // 顶点 v2：地图点，顶点的 id 为 0.
    const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
    // 观测值：特征点在当前帧中的像素坐标.
    Vector2d obs(_measurement);
    // 计算误差：观测-重投影.
    _error = obs-cam_project(v1->estimate().map(v2->estimate()));
  }

  // 检查地图点在相机坐标系中深度是否为正.
  bool isDepthPositive() 
  {
    const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
    const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);
    return (v1->estimate().map(v2->estimate()))(2)>0.0;
  }

  // 构造雅克比矩阵：重投影误差相对于相机坐标和地图点的一阶导.
  virtual void linearizeOplus();

  // 投影到当前帧.
  Vector2d cam_project(const Vector3d & trans_xyz) const;

  double fx, fy, cx, cy;
}; // 边：重投影误差（BA优化时）.

其中 linearizeOplus() 函数用于构造雅克比矩阵，需要重投影误差对相机位姿和地图点求一阶偏导，对应 g2o/types/types_six_dof_expmap.cpp 中的 void EdgeSE3ProjectXYZ::linearizeOplus() 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


// BRIEF 重投影误差的雅克比矩阵（BA 优化时相对于相机位姿和地图点的一阶导）
void EdgeSE3ProjectXYZ::linearizeOplus() 
{
  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat T(vj->estimate());
  VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
  Vector3d xyz = vi->estimate();
  Vector3d xyz_trans = T.map(xyz);

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double z = xyz_trans[2];
  double z_2 = z*z;

  Matrix<double,2,3> tmp;
  tmp(0,0) = fx;
  tmp(0,1) = 0;
  tmp(0,2) = -x/z*fx;

  tmp(1,0) = 0;
  tmp(1,1) = fy;
  tmp(1,2) = -y/z*fy;

  _jacobianOplusXi =  -1./z * tmp * T.rotation().toRotationMatrix();

  _jacobianOplusXj(0,0) =  x*y/z_2 *fx;
  _jacobianOplusXj(0,1) = -(1+(x*x/z_2)) *fx;
  _jacobianOplusXj(0,2) = y/z *fx;
  _jacobianOplusXj(0,3) = -1./z *fx;
  _jacobianOplusXj(0,4) = 0;
  _jacobianOplusXj(0,5) = x/z_2 *fx;

  _jacobianOplusXj(1,0) = (1+y*y/z_2) *fy;
  _jacobianOplusXj(1,1) = -x*y/z_2 *fy;
  _jacobianOplusXj(1,2) = -x/z *fy;
  _jacobianOplusXj(1,3) = 0;
  _jacobianOplusXj(1,4) = -1./z *fy;
  _jacobianOplusXj(1,5) = y/z_2 *fy;
} // 重投影误差的雅克比矩阵（BA 优化时相对于相机位姿和地图点的一阶导）

4.3 闭环检测时的重投影误差

闭环检测时执行 sim3 优化，边是重投影误差，顶点是 sim3 表示的相机位姿和地图点坐标，对应 g2o/types/types_seven_dof_expmap.h 中定义的边投影到当前帧 EdgeSim3ProjectXYZ 和投影到闭环帧 EdgeInverseSim3ProjectXYZ。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


// BRIEF 边：重投影误差（闭环检测时）顶点：地图点坐标，sim3 表示的相机位姿.
class EdgeSim3ProjectXYZ : public  BaseBinaryEdge<2, Vector2d,  VertexSBAPointXYZ, VertexSim3Expmap>
{
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    EdgeSim3ProjectXYZ();
    virtual bool read(std::istream& is);
    virtual bool write(std::ostream& os) const;

    // 重投影误差计算.
    void computeError()
    {
      const VertexSim3Expmap* v1 = static_cast<const VertexSim3Expmap*>(_vertices[1]);
      const VertexSBAPointXYZ* v2 = static_cast<const VertexSBAPointXYZ*>(_vertices[0]);

      Vector2d obs(_measurement);
      _error = obs-v1->cam_map1(project(v1->estimate().map(v2->estimate())));
    }

    // TODO 这里继承的 BaseBinaryEdge 雅克比矩阵构造函数？.
    // virtual void linearizeOplus();
};

4.4 Sim3 之间的相对误差

OptimizeEssentialGraph 会在成功进行闭环检测后、全局 BA 优化前进行，边为 Sim3 之间的相对误差，顶点为 Sim3 表示的相机位姿。对应 g2o/types/types_seven_dof_expmap.h 中定义的边 EdgeSim3。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


// BRIEF 边：Sim3 之间的相对误差，顶点：Sim3 表示的 pose。（OptimizeEssentialGraph 优化中）
  class EdgeSim3 : public BaseBinaryEdge<7, Sim3, VertexSim3Expmap, VertexSim3Expmap>
  {
  public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW

    EdgeSim3();
    virtual bool read(std::istream& is);
    virtual bool write(std::ostream& os) const;

    // 误差计算.
    void computeError()
    {
      const VertexSim3Expmap* v1 = static_cast<const VertexSim3Expmap*>(_vertices[0]);
      const VertexSim3Expmap* v2 = static_cast<const VertexSim3Expmap*>(_vertices[1]);

      Sim3 C(_measurement);
      Sim3 error_=C*v1->estimate()*v2->estimate().inverse();
      _error = error_.log();
    }

    virtual double initialEstimatePossible(const OptimizableGraph::VertexSet& , OptimizableGraph::Vertex* ) { return 1.;}

    virtual void initialEstimate(const OptimizableGraph::VertexSet& from, OptimizableGraph::Vertex* /*to*/)
    {
      VertexSim3Expmap* v1 = static_cast<VertexSim3Expmap*>(_vertices[0]);
      VertexSim3Expmap* v2 = static_cast<VertexSim3Expmap*>(_vertices[1]);
      if (from.count(v1) > 0)
        v2->setEstimate(measurement()*v1->estimate());
      else
        v1->setEstimate(measurement().inverse()*v2->estimate());
    }
  }; // 边：Sim3 之间的相对误差，顶点：Sim3 表示的 pose。（OptimizeEssentialGraph 优化中）

5. ORB-SLAM2 中的优化函数

5.1 位姿优化函数 PoseOptimization()

函数描述：
- 在 Tracking 线程中进行位姿优化的时候，每进行过一次 PnP 投影操作将地图点投影到当前平面上之后，都会进行一次PoseOptimization 位姿优化最小化重投影误差；
- 3D-2D 最小化重投影误差 e = (u,v) - project(Tcw*Pw)；
- 只优化当前帧 pose，地图点固定；
- 用于 LocalTracking 中运动模型跟踪，参考帧跟踪，地图跟踪 TrackLocalMap，重定位。

顶点和边：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


1. Vertex: g2o::VertexSE3Expmap()，即当前帧的 Tcw
2. Edge: 重投影误差（一元边）
 - 单目情况：g2o::EdgeSE3ProjectXYZOnlyPose()，BaseUnaryEdge
     + Vertex：待优化当前帧的Tcw
     + measurement：MapPoint在当前帧中的二维位置(u,v)
     + InfoMatrix: invSigma2(与特征点所在的尺度有关)
 - 双目情况：g2o::EdgeStereoSE3ProjectXYZOnlyPose()，BaseUnaryEdge
     + Vertex：待优化当前帧的Tcw
     + measurement：MapPoint在当前帧中的二维位置(ul,v,ur)
     + InfoMatrix: invSigma2(与特征点所在的尺度有关)

函数执行流程：

步骤一： 构造 g2o 优化器
步骤二： 向优化器中添加顶点-当前帧的位姿

步骤三： 向优化器中添加边（以单目重投影误差为例）

步骤 1： 实例化一个 EdgeSE3ProjectXYZOnlyPose 一元边

1

g2o::EdgeSE3ProjectXYZOnlyPose* e = new g2o::EdgeSE3ProjectXYZOnlyPose();

步骤 2： 设置边连接的顶点

1

e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0)));

步骤 3： 添加边的观测值（2D）

1

e->setMeasurement(obs);     // 观测：地图点在当前帧中的像素坐标.

步骤 4： 设置边的信息矩阵

1
2
3


const float invSigma2 = pFrame->mvInvLevelSigma2[kpUn.octave];
// note 设置权重（信息矩阵），与特征点金字塔有关，参考：https://www.zhihu.com/question/58762862
e->setInformation(Eigen::Matrix2d::Identity()*invSigma2);   // 信息矩阵（权重）

步骤 5： 设置核函数

步骤 6： 获取地图点的世界坐标（3D）

1
2
3
4


cv::Mat Xw = pMP->GetWorldPos();
e->Xw[0] = Xw.at<float>(0);
e->Xw[1] = Xw.at<float>(1);
e->Xw[2] = Xw.at<float>(2);

步骤 7： 将边添加到优化器中。

步骤四：开始优化，共优化 4 次，每次优化后将观测分为 outlier 和 inlier，outlier 不参与下次优化。
- 但由于每次优化后是对所有的观测进行outlier和inlier判别，因此之前被判别为outlier有可能变成inlier，反之亦然。
- 基于卡方检验计算异常值的阈值（假设测量有一个像素的偏差）。
步骤五： 优化结束，用优化之后的位姿更新当前帧的位姿。

5.2 局部优化 LocalBundleAdjustment()

函数描述
- 执行条件：在已经处理完队列中的最后一个关键帧之后，并且闭环检测线程没有请求停止局部建图线程，则开始对当前帧进行局部 BA 优化，或者当新的关键帧加入到 convisibility graph 时，在关键帧附近进行一次局部优化，如下图所示；
  - Pos3 是新加入的关键帧，其初始估计位姿已经得到，此时，Pos2 是和 Pos3 相连的关键帧，X2 是 Pos3 看到的三维点，X1 是 Pos2 看到的三维点，这些都属于局部信息，共同参与Bundle Adjustment（圈内红色部分）；
  - 同时，Pos1 也可以看到 X1，但它和 Pos3 没有直接的联系，属于 Pos3 关联的局部信息，参与 Bundle Adjustment，但取值保持不变（圈内灰色部分）；
  - Pos0 和 X0 不参与 Bundle Adjustment（圈外灰色部分）。
  - 因此，参与优化的是上图中红色椭圆圈出的部分，其中红色代表取值会被优化，灰色代表取值保持不变。(u,v) 是 X 在 Pos 下的二维投影点，即 X 在 Pos 下的测量（measurement），优化的目标是让投影误差最小。

顶点与边

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


1. Vertex:
    - g2o::VertexSE3Expmap()，LocalKeyFrames，即当前关键帧一级与当前关键帧相连的关键帧的位姿
    - g2o::VertexSE3Expmap()，FixedCameras，即能观测到LocalMapPoints的关键帧（并且不属于LocalKeyFrames）的位姿，在优化中这些关键帧的位姿不变
    - g2o::VertexSBAPointXYZ()，LocalMapPoints，即LocalKeyFrames能观测到的所有MapPoints的位置
2. Edge:
    - 单目 g2o::EdgeSE3ProjectXYZ()，BaseBinaryEdge
        + Vertex：关键帧的Tcw，MapPoint的Pw
        + measurement：MapPoint在关键帧中的二维位置(u,v)
        + InfoMatrix: invSigma2(与特征点所在的尺度有关)
    - 双目 g2o::EdgeStereoSE3ProjectXYZ()，BaseBinaryEdge
        + Vertex：关键帧的Tcw，MapPoint的Pw
        + measurement：MapPoint在关键帧中的二维位置(ul,v,ur)
        + InfoMatrix: invSigma2(与特征点所在的尺度有关)

函数执行流程

步骤一：构造局部关键帧列表

步骤 1：将当前帧加入到列表中

1
2


list<KeyFrame*> lLocalKeyFrames;
lLocalKeyFrames.push_back(pKF);

步骤 2：将与当前关键帧一级相连的关键帧加入到列表中

1

const vector<KeyFrame*> vNeighKFs = pKF->GetVectorCovisibleKeyFrames();

步骤二：构造局部地图点列表。遍历前面的局部关键帧列表 lLocalKeyFrames，得到每个关键帧锁观测到的地图点，加入到局部地图点列表 lLocalMapPoints 中。
步骤三：构造能被局部地图点观测到的但不属于局部关键帧列表的关键帧 lFixedCameras 。这些关键帧参与局部 BA 但不改变其值。
步骤四：构造 g2o 优化器

步骤五：向优化器中添加顶点 VertexSE3Expmap - 局部关键帧。遍历局部关键帧序列 lLocalKeyFrames，将其创建为顶点，添加到优化器中

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


// 实例化一个 VertexSE3Expmap 顶点的对象.
g2o::VertexSE3Expmap * vSE3 = new g2o::VertexSE3Expmap();
      
// 设置顶点的关键帧位姿属性（SE3 形式）、ID 和固定的顶点.
vSE3->setEstimate(Converter::toSE3Quat(pKFi->GetPose()));
vSE3->setId(pKFi->mnId);
vSE3->setFixed(pKFi->mnId==0); //第一帧位置固定
      
// 将顶点添加到的优化器中.
optimizer.addVertex(vSE3);

步骤六：向优化器中添加顶点 VertexSE3Expmap - 不修改值的关键帧。遍历前面构造的 lFixedCameras，分别对齐创建为顶点，注意 setFixed(true) 不改变其值

1
2
3
4
5


g2o::VertexSE3Expmap * vSE3 = new g2o::VertexSE3Expmap();
vSE3->setEstimate(Converter::toSE3Quat(pKFi->GetPose()));
vSE3->setId(pKFi->mnId);
vSE3->setFixed(true);
optimizer.addVertex(vSE3);

步骤七：向优化器中添加顶点 VertexSBAPointXYZ - 地图点。遍历前面的局部地图点列表，依次创建顶点

1
2
3
4
5
6
7
8
9


// 实例化一个 VertexSBAPointXYZ 顶点.
g2o::VertexSBAPointXYZ* vPoint = new g2o::VertexSBAPointXYZ();
// 设置顶点的位置、ID，边缘化.
vPoint->setEstimate(Converter::toVector3d(pMP->GetWorldPos()));
int id = pMP->mnId+maxKFid+1;
vPoint->setId(id);
vPoint->setMarginalized(true);
// 将顶点添加到优化器中.
optimizer.addVertex(vPoint);

步骤八：为每一对关联的地图点和关键帧创建边（与上一步构建地图点顶点一起创建，以单目为例）。

步骤 1：实例化一条二元边 EdgeSE3ProjectXYZ

1

g2o::EdgeSE3ProjectXYZ* e = new g2o::EdgeSE3ProjectXYZ();

步骤 2：为边添加关联的顶点

1
2


e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id)));// 地图点 ID.
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKFi->mnId)));// 关键帧 ID.

步骤 3：添加测量值

1

e->setMeasurement(obs);     // 测量：地图点在当前帧中的二维位置.

步骤 4：构造信息矩阵

1
2


const float &invSigma2 = pKFi->mvInvLevelSigma2[kpUn.octave]; // 与特征点所在的尺度有关.
e->setInformation(Eigen::Matrix2d::Identity()*invSigma2);   // 设置信息矩阵.

步骤 5：设置核函数
步骤 6：将边添加到优化器中

步骤九：开始执行优化，迭代 5 次

1
2


optimizer.initializeOptimization();
optimizer.optimize(5);      // 迭代 5 次.

步骤十：检测 outlier，并设置下次不优化，同前面位姿优化时一样采用卡方检验计算阈值。
步骤十一：排除误差较大的 outlier 后再次优化，迭代 10 次
1 2

optimizer.initializeOptimization(0); optimizer.optimize(10);
步骤十二：在优化后重新计算误差，剔除连接误差比较大的关键帧和地图点。
步骤十三：优化后更新关键帧位姿以及地图点坐标、平均观测方向等属性。

5.3 全局优化 GlobalBundleAdjustemnt()

函数描述
- 全局 BA 优化在单目初始化和闭环矫正时执行。在全局优化中，所有的关键帧（除了第一帧）和三维点都参与优化，如下图所示：

顶点与边

1
2
3
4
5
6
7
8
9


3D-2D 最小化重投影误差 e = (u,v) - project(Tcw*Pw)
1. Vertex: g2o::VertexSE3Expmap()，即当前帧的Tcw
           g2o::VertexSBAPointXYZ()，MapPoint 的 mWorldPos
2. Edge:
    - g2o::EdgeSE3ProjectXYZ()，BaseBinaryEdge
        + Vertex：待优化当前帧的Tcw
        + Vertex：待优化MapPoint的mWorldPos
        + measurement：MapPoint在当前帧中的二维位置(u,v)
        + InfoMatrix: invSigma2(与特征点所在的尺度有关)

函数执行流程

步骤一：构造 g2o 优化器。

步骤二：向优化器中添加顶点 VertexSE3Expmap - 关键帧的位姿。 遍历系统关键帧列表中的所有关键帧，依次添加顶点。

1
2
3
4
5


g2o::VertexSE3Expmap * vSE3 = new g2o::VertexSE3Expmap();
vSE3->setEstimate(Converter::toSE3Quat(pKF->GetPose()));
vSE3->setId(pKF->mnId);
vSE3->setFixed(pKF->mnId==0); // 固定第一帧的位姿，其它帧可修正位姿
optimizer.addVertex(vSE3);

步骤三：向优化器中添加顶点 VertexSBAPointXYZ - 地图点坐标。遍历所有关键帧观察到的地图点，依次添加为顶点

1
2
3
4
5
6


g2o::VertexSBAPointXYZ* vPoint = new g2o::VertexSBAPointXYZ();
vPoint->setEstimate(Converter::toVector3d(pMP->GetWorldPos()));
const int id = pMP->mnId+maxKFid+1;
vPoint->setId(id);
vPoint->setMarginalized(true);
optimizer.addVertex(vPoint);

步骤四：向优化器中添加边 EdgeSE3ProjectXYZ - 重投影误差。

步骤 1：实例化一条边

1

g2o::EdgeSE3ProjectXYZ* e = new g2o::EdgeSE3ProjectXYZ();

步骤 2：添加顶点

1
2


e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id)));
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKF->mnId)));

步骤 3：添加测量值

1
2
3


Eigen::Matrix<double,2,1> obs;
obs << kpUn.pt.x, kpUn.pt.y;
e->setMeasurement(obs);

步骤 4：设置信息矩阵

1
2


const float &invSigma2 = pKF->mvInvLevelSigma2[kpUn.octave];
e->setInformation(Eigen::Matrix2d::Identity()*invSigma2);

步骤 5：设置核函数
步骤 6：添加到优化器中

步骤五：开始优化，迭代 20 次。
步骤六：更新优化结果（关键帧位姿、地图点坐标）。

5.4 闭环处的 Sim3 优化 OptimizeSim3()

函数描述
- 在用 RANSAC 求解过 Sim3，以及通过 Sim3 匹配更多的地图点后，对当前关键帧，闭环关键帧，以及匹配的地图点进行优化，获得更准确的 Sim3 变换，再进行下一步的闭环调整；
- 当检测到闭环时，闭环连接的两个关键帧的位姿需要通过 Sim3 优化（以使得其尺度一致），在函数 Optimizer::OptimizeSim3() 中实现，优化求解两帧之间的相似变换矩阵，使得二维对应点的投影误差最小；
- 如下图所示，Pos6 和 Pos2 为一个可能的闭环，则通过 $(u_{4,2},v_{4,2})$ 和 $(u_{4,6},v_{4,6})$ 之间的投影误差来优化 $S_{6,2}$。

顶点与边

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


1. Vertex:
    - g2o::VertexSim3Expmap()，两个关键帧的位姿
    - g2o::VertexSBAPointXYZ()，两个关键帧共有的 MapPoints
2. Edge:
    - g2o::EdgeSim3ProjectXYZ()，BaseBinaryEdge，投影到当前帧
         + Vertex：关键帧的Sim3，MapPoint的Pw
         + measurement：MapPoint在关键帧中的二维位置(u,v)
         + InfoMatrix: invSigma2(与特征点所在的尺度有关)
    - g2o::EdgeInverseSim3ProjectXYZ()，BaseBinaryEdge，投影到闭环帧
         + Vertex：关键帧的Sim3，MapPoint的Pw
         + measurement：MapPoint在关键帧中的二维位置(u,v)
         + InfoMatrix: invSigma2(与特征点所在的尺度有关)

函数执行流程

步骤一： 初始化 g2o 优化器；

步骤二：添加顶点 VertexSim3Expmap - sim3 位姿，顶点的值为两个关键帧之间的 sim3 变换；

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


g2o::VertexSim3Expmap * vSim3 = new g2o::VertexSim3Expmap();    
vSim3->_fix_scale=bFixScale;
vSim3->setEstimate(g2oS12);     // 两个关键帧间的Sim3变换
vSim3->setId(0);
vSim3->setFixed(false);// 优化Sim3顶点
vSim3->_principle_point1[0] = K1.at<float>(0,2); // 光心横坐标cx
vSim3->_principle_point1[1] = K1.at<float>(1,2); // 光心纵坐标cy
vSim3->_focal_length1[0] = K1.at<float>(0,0); // 焦距 fx
vSim3->_focal_length1[1] = K1.at<float>(1,1); // 焦距 fy
vSim3->_principle_point2[0] = K2.at<float>(0,2);
vSim3->_principle_point2[1] = K2.at<float>(1,2);
vSim3->_focal_length2[0] = K2.at<float>(0,0);
vSim3->_focal_length2[1] = K2.at<float>(1,1);
optimizer.addVertex(vSim3);

步骤三：添加顶点 VertexSBAPointXYZ - 两帧的共视地图点，顶点的值为地图点的相机坐标；
步骤四：添加边 - 顶点投影到当前帧的重投影误差 EdgeSim3ProjectXYZ 和投影到闭环帧的重投影误差 EdgeInverseSim3ProjectXYZ；
步骤五： 开始优化，迭代 5 次；
步骤六： 卡方检验剔除误差较大的边；
步骤七： 再次优化剩余的边，迭代 5 或者 10 次；
步骤八： 优化结束，返回两帧之间的 sim3 变换。

5.5 闭环后的 Sim3 位姿优化 OptimizeEssentialGraph()

函数描述
- 单目 SLAM 一般都会发生尺度（scale）漂移，因此 Sim3 上的优化是必要的，相对于SE3，Sim3 的自由度要多一个，而且优化的目标是矫正尺度因子，因此优化并没有加入更多的变量（如三维点）；
- 在检测到闭环时在 sim3 上对所有的位姿进行一次优化，在函数 Optimizer::OptimizeEssentialGraph() 中执行，EssentialGraph 包括所有的关键帧顶点，但是优化边大大减少，包括 spanning tree（生成树），共视权重θ>100 的边，以及闭环连接边。用于闭环检测 Sim3 调整后优化。
- 定义 sim3 上的残差为： $$ e_{i,j}=log_{Sim3}(S_{ij}S_{jw}S_{iw}^{-1}) $$
- 其中 $S_{iw}$ 的初值是尺度为 1 的 pos i 相对于世界坐标系的变换矩阵，$S_{jw}$ 同理；
- $S_{ij}$ 表示 pos i 和 pos j 之间的相对位姿矩阵（sim3 优化之前），表示 $S_{iw}$ 和 $S_{jw}$ 之间的测量；
- 此处相当于认为局部的相对位姿是准确的，而全局位姿有累计误差，是不准确的

顶点与边

1
2
3
4
5
6
7


1. Vertex:
    - g2o::VertexSim3Expmap，Essential graph中关键帧的位姿
2. Edge:
    - g2o::EdgeSim3()，BaseBinaryEdge
        + Vertex：关键帧的Tcw，MapPoint的Pw
        + measurement：经过CorrectLoop函数步骤2，Sim3传播校正后的位姿
        + InfoMatrix: 单位矩阵   

函数执行流程
- 步骤一： 初始化 g2o 优化器；
- 步骤二： 添加顶点 VertexSim3Expmap - 地图中所有的关键帧；
- 步骤三： 添加边
  - 闭环时因为 MapPoints 调整而出现的新关键帧之间的 sim3 变换误差
  - 当前帧与闭环匹配成功的帧之间的误差
- 步骤四： 开始优化，迭代 20 次；
- 步骤五： 优化结束更新位姿 Sim3:[sR t;0 1] -> SE3:[R t/s;0 1]；
- 步骤六： MapPoints 根据参考帧优化前后的相对关系调整自己的位置（地图点坐标不是直接从优化器中更新的）。

R. 参考资料

TODO

5.4，5.5 这两个闭环时的优化函数没太理解，后面专门做一个关于闭环的总结把这两个函数带上。

2019.07.05
wuyanminmax@gmail.com

文章目录

0. 基本使用

0.1 构造 g2o 模型

0.2 g2o 类图

1. g2o 的顶点（Vertex）

1.1 顶点的格式

1.2 自定义顶点

1.3 将顶点添加到图中

2. g2o 中的边

2.1 边的格式

2.2 自定义边

2.3 将边添加到图中

3. ORB-SLAM2 中的顶点

3.1 相机位姿顶点

3.2 地图点坐标顶点

3.3 闭环时的 sim3 相机位姿

4. ORB-SLAM2 中的边

4.1 位姿优化时的重投影误差

4.2 BA 优化时的重投影误差

4.3 闭环检测时的重投影误差

4.4 Sim3 之间的相对误差

5. ORB-SLAM2 中的优化函数

5.1 位姿优化函数 PoseOptimization()

5.2 局部优化 LocalBundleAdjustment()

5.3 全局优化 GlobalBundleAdjustemnt()

5.4 闭环处的 Sim3 优化 OptimizeSim3()

5.5 闭环后的 Sim3 位姿优化 OptimizeEssentialGraph()

R. 参考资料

TODO