😀 ORB-SLAM2 代码解读（三）：单目初始化
文章目录
单目初始化通过并行地计算基础矩阵 F 和单应矩阵 H ，恢复出最开始两帧的匹配、相机初始位姿，三角化得到 MapPoints 的深度，获得初始化点云地图，并对恢复的点云和相机位姿做全局 BA。
同时计算两个模型：
用于平面场景的单应性矩阵 H（4对 3d-2d点对，线性方程组，奇异值分解）
用于非平面场景的基础矩阵 F（8对 3d-2d点对，线性方程组，奇异值分解） 0. 算法流程
步骤一： 创建单目初始器并获取第一帧图像（未创建初始器）
- 步骤 1： 对当前帧特征点数量进行判断，要求特征点数必须大于 100，满足则作为初始化的第一帧，用
mInitialFrame表示第一帧（初始帧）， mLastFrame 表示上一帧，mvbPrevMatched用于存储第一帧中的所有特征点； - 步骤 2： ==Initializer::Initializer()== 创建初始器，获取相机内参、参考帧的特征点，初始化估计误差和最大的 RANSAC 迭代次数:；
- 用
mvIniMatches表示两帧之间的匹配标志，先填充为 -1 ，也就是均没有匹配。
- 步骤 1： 对当前帧特征点数量进行判断，要求特征点数必须大于 100，满足则作为初始化的第一帧，用
步骤二： 获取单目初始化的第二帧（单目初始化器已经被创建）
- 要求这一帧的特征点数也要大于 100 ，如果小于 100 个，则删除单目初始器 Initializer ，回到步骤一重新创建；
- 也就是只有连续两帧的特征点个数都大于100时，才能继续进行初始化过程。
- NOTE：步骤一二比较的特征点都是未经畸变矫正的点
mCurrentFrame.mvKeys。
步骤三： 在 mInitialFrame 与 mCurrentFrame 中通过图像网格加速寻找匹配的特征点对
- 创建特征匹配器并利用 ==
ORBmatcher::SearchForInitialization()== 函数进行金字塔分层块匹配搜索匹配点对，返回匹配的数目；
// 创建特征匹配器. ORBmatcher matcher( 0.9, true); // 第一个参数：最佳匹配与次佳匹配的比值，默认为 0.6；第二个参数：是否检查特征点的方向. // 针对单目初始化的时候,进行特征点的匹配 int nmatches = matcher.SearchForInitialization( mInitialFrame, mCurrentFrame, // 初始化时的参考帧和当前帧 mvbPrevMatched, // 在初始化参考帧中提取得到的特征点 mvIniMatches, // 匹配标志 100); // 搜索窗口的大小- 调用 ==
ORBmatcher::DescriptorDistance()== 函数比较两帧之间的描述子距离，确保距离小于 ORBmatcher::TH_LOW = 50； - SearchForInitialization() 的功能：根据可能匹配特征点的描述子计算距离，确定最佳匹配；另外如果考虑特征点的方向，则将第一帧中的特征的方向角度减去对应第二帧的特征的方向角度，将值划分为直方图，则会在 0 度和 360 度左右对应的组距比较大，这样就可以对其它相差太大的角度可以进行剔除；
- 函数返回的匹配数 nmatches 小于 100，则回到步骤一，重新初始化，若大于 100，则进行后续初始化。
- 创建特征匹配器并利用 ==
步骤四： ==
Initializer::Initialize()== 并行计算 H 模型或 F 模型进行单目初始化，得到两帧间相对运动、初始MapPoints- 步骤 1： 筛选出匹配的点对，
mvIniMatches存储匹配标志，将标志 >= 0 的点索引关系保存到 mvMatches12
步骤 2： 在所有匹配特征点对中随机选择 8 对匹配特征点为一组，共选择
Initializer::mMaxIterations组，其中 mMaxIterations 是最大的 RANSAC迭代次数，在初始化初始器的时候赋值为 200；- 产生的点对保存在 mvSets 中，用于保存每次迭代时所使用的向量，保存八对点进行单应矩阵和基础矩阵估计（求解矩阵使用八点法），迭代 mMaxIterations 次，每次迭代随机挑选 8 个点（不重复）
步骤 3： 多线程计算基础矩阵和单应矩阵
// 计算 homography 矩阵并打分. thread threadH( &Initializer::FindHomography, // 计算单应矩阵的函数 this, //NOTE 由于主函数为类的成员函数，所以第一个参数就应该是当前对象的this指针 ref(vbMatchesInliersH), //输出，特征点对的 Inlier 标记 ref(SH), //输出，计算的单应矩阵的 RANSAC 评分 ref(H)); //输出，计算的单应矩阵结果 // 计算 fundamental 矩阵并打分. thread threadF(&Initializer::FindFundamental,this,ref(vbMatchesInliersF), ref(SF), ref(F));- 线程一： 计算单应矩阵及其得分 ==
Initializer::FindHomography()==- 步骤 ①：利用 ==
Initializer::Normalize()== 函数归一化特征点的尺度，固定场景尺度； - 步骤 ②：利用 ==
Initializer::ComputeH21()== 函数八点法计算 homography 矩阵； - 步骤 ③：利用 ==
Initializer::CheckHomography()== 函数求取 利用重投影误差为 RANSAC 的结果评分； - 步骤 ④：记录最大的得分。
- 步骤 ①：利用 ==
- 线程二： 计算本质矩阵及其得分 ==
Initializer::FindFundamental()==- 步骤 ①：利用 ==
Initializer::Normalize()== 函数归一化特征点的尺度，固定场景尺度； - 步骤 ②：利用 ==
Initializer::ComputeF21()== 函数八点法计算 fundamental 矩阵； - 步骤 ③：利用 ==
Initializer::CheckFundamental()== 函数求取 利用重投影误差为 RANSAC 的结果评分； - 步骤 ④：记录最大的得分。
- 步骤 ①：利用 ==
- 线程一： 计算单应矩阵及其得分 ==
步骤 4： 计算两个矩阵的得分比，判断选择哪个模型，判断谁的评分占比更多一些，注意不是简单的评分大，而是看评分的占比。
- 步骤 5： 从选择的 F 矩阵或 H 矩阵中恢复当前帧相对于第一帧的位姿 R,t完成初始化；
- 情形一： RH > 0.40，偏向于平面，从单应矩阵恢复 ==
Initializer::ReconstructH()==； - 情形二： RF > 0.60，偏向于非平面，从基础矩阵恢复 ==
Initializer::ReconstructF()==。- 步骤 ①：将基础矩阵转换成本质矩阵 E；
- 步骤 ②：对本质矩阵进行分解，得到两个 R 和两个 t ==
Initializer::DecomposeE==； - 步骤 ③：依次检查四组解情况下 3D 点在摄像头前方且投影误差小于阈值的 3D 点个数，==
Initializer::CheckRT()==；- 步骤 A： 计算两帧下的投影矩阵 P1，P2；
- 步骤 B： 2D 点和投影矩阵作为输入进行三角化恢复 3D 点 ==
Initializer::Triangulate()== - 步骤 C： 检验三角化的 3D 点是否符合要求
- 检验一： 如果三角测量的结果中有一个是无穷大的就说明三角化失败；
- 检验二： 判断 3D 点是否在两个摄像头前方，视差角是否足够大；
if(p3dC1.at<float>(2)<=0 && // 3D点深度为负 cosParallax<0.99998) // 并且还要有一定的视差角，一般视差角比较小时重投影误差比较大 continue;- 检验三： 计算空间点在参考帧和当前帧上的重投影误差，需要小于阈值
// NOTE 计算3D点在第一个图像上的投影误差 // 投影到参考帧图像上的点的坐标x,y float im1x, im1y; // 这个使能空间点的z坐标的倒数 float invZ1 = 1.0/p3dC1.at<float>(2); // 投影到参考帧图像上。因为参考帧下的相机坐标系和世界坐标系重合，因此这里就直接进行投影就可以了 im1x = fx*p3dC1.at<float>(0)*invZ1+cx; im1y = fy*p3dC1.at<float>(1)*invZ1+cy; // 参考帧上的重投影误差，这个的确就是按照定义来的 float squareError1 = (im1x-kp1.pt.x)*(im1x-kp1.pt.x)+(im1y-kp1.pt.y)*(im1y-kp1.pt.y); // 重投影误差太大，跳过淘汰，一般视差角比较小时重投影误差比较大 if(squareError1>th2) continue; // 后面同样计算 3D 点在第二个图像上的投影误差，略 - 步骤 D： 统计满足上面三个条件的 3D 点，被称为 goog 点，并将视差从小到大排序，记录第 50 小的视差值（若少于 50 则取最后一个）。
- 步骤 ④：检查是否有足够大的视差角，选择视差角大于阈值,并且满足条件的 3D 点个数明显大于其它模型的一组 [R,t] 解作为结果。
- 情形一： RH > 0.40，偏向于平面，从单应矩阵恢复 ==
- 步骤 1： 筛选出匹配的点对，
步骤五： 删除无法三角化的匹配点，其中
mvIniMatches是两帧之间特征点的匹配标志，vbTriangulated是其对应的三角化标志。
for(size_t i=0, iend = mvIniMatches.size(); i<iend;i++)
{
if(mvIniMatches[i]>=0 && !vbTriangulated[i])
{
mvIniMatches[i]=-1;
nmatches--;
}
}- 步骤六： 设置初始两帧的世界坐标位姿
- 初始帧的位姿设置为单位矩阵
- 当前帧（第二帧）的位姿有前面矩阵恢复出的 R,t 构造
- 步骤七： ==
Tracking::CreateInitialMapMonocular()== 将三角化得到的点包装成地图点 MapPoints，创建初始地图，使用最小化重投影误差 BA 进行地图优化，优化位姿和地图点；- 步骤 1： 创建初始关键帧，认为单目初始化时候的参考帧和当前帧都是关键帧 ==
KeyFrame::KeyFrame()==
KeyFrame* pKFini = new KeyFrame(mInitialFrame, mpMap, mpKeyFrameDB); KeyFrame* pKFcur = new KeyFrame(mCurrentFrame, mpMap, mpKeyFrameDB);- 步骤 2： 将初始化的两帧关键帧的描述子转换成 BoW ==
Frame::ComputeBoW()==
- 步骤 3： 将关键帧插入到地图，凡是关键帧都需要插入到地图 ==
Map::AddKeyFrame(KeyFrame *pKF)==
- 步骤 4： 将 3D 点包装成 MapPoints
- 步骤 ①：构造地图点 ==
MapPoint::MapPoint()==
- 步骤 ②：添加地图点到关键帧 ==
KeyFrame::AddMapPoint(MapPoint *pMP, const size_t &idx)==
pKFini->AddMapPoint(pMP,i); // 第一个参数是地图点，第二个参数是地图点在关键帧中的索引. pKFcur->AddMapPoint(pMP,mvIniMatches[i]);- 步骤 ③：记录关键帧的哪个特征点能观察到该地图点； ==
MapPoint::AddObservation(KeyFrame* pKF, size_t idx)==
- 步骤 ④：从众多观测到该 MapPoint 的特征点中挑选区分度最高的描述子 ==
MapPoint::ComputeDistinctiveDescriptors()== - 步骤 ⑤：更新该 MapPoint 平均观测方向以及观测距离的范围 ==
MapPoint::UpdateNormalAndDepth()== - 步骤 ⑥：在地图中添加该 MapPoint ==
AddMapPoint(MapPoint *pMP)==
- 步骤 ①：构造地图点 ==
- 步骤 5： 更新关键帧间的连接关系 ==
KeyFrame::UpdateConnections()==- 在 3D 点和关键帧之间建立边，每个边有一个权重，边的权重是该关键帧与当前帧公共 3D 点的个数
- 步骤 6： BA 优化 ==
Optimizer::GlobalBundleAdjustemnt()== - 步骤 7： 将 MapPoints 的中值深度归一化到1，并归一化两帧之间变换；
- 步骤 8： 更新状态量，包括关键帧、地图点信息，更新地图绘制器。
- 步骤 1： 创建初始关键帧，认为单目初始化时候的参考帧和当前帧都是关键帧 ==
- 单目初始化结束。
1. 初始两帧的特征匹配
对应于算法流程中的步骤三，参考：ORB-SLAM2 初始化时两帧之间的特征匹配 SearchForInitialization()
2. Fundamental 基本矩阵求解变换
2.1 归一化特征点坐标
8 点法是计算基本矩阵最简单的方法。为了提高解的稳定性和精度，通常需要对输入的点集坐标进行归一化处理（吴博师兄在视频中提到好像是为了防止不同分辨率、尺度和坐标原点下的影响）。 + 在 MVG 的估计一章中推荐各向同性归一化，OpenCV的8点算法也是使用了各向同性，也就是使得各个点做平移缩放之后到坐标原点的均方根距离等于 \(\sqrt 2\); + 各向同性归一化和非各向同性归一化在论文 In Defense of the Eight-Point Algorithm 中有讨论，ORB-SLAM2 单目初始化 F 矩阵计算之前的归一化使用的是非各向同性归一化。（上面这段文字来自于许可师兄博客）
- 步骤一： 求取所有 N 个特征点的质心坐标（X, Y） \[ meanX = \frac{\sum_{N}^{i=0}u_{i}}{N},\quad meanY = \frac{\sum_{N}^{i=0}v_{i}}{N} \]
- 步骤二： 计算所有点相对于质心的平均距离 \[
meanDevX = \frac{\sum_{N}^{i=0}\left | u_{i}-meanX \right |}{N},\quad meanDevY = \frac{\sum_{N}^{i=0}\left | v_{i}-meanY \right |}{N}
\]
- 并将平均距离的倒数作为缩放尺度因子 \[ sX = \frac{1}{meanDevX} ,\quad sY = \frac{1}{meanDevY} \]
- 步骤三： 对特征点的 x 和 y 坐标进行缩放，使得一阶绝对矩为 1，以此作为归一化的结果坐标 \[ x=x\cdot sX, \quad y = y \cdot sY \]
- 步骤四： 获得归一化矩阵 T（由 x y 方向的缩放因子和归一化的特征点质心组成） \[
T = \begin{bmatrix}
sX &0 & -meanX\cdot sX\\
0 & sY & -meanY\cdot sY\\
0 & 0 & 1
\end{bmatrix}
\] 关于一阶绝对矩
什么是矩？ 在统计学中，矩表征随机量的分布。
一阶矩是随机变量的期望，二阶矩是随机变量平方的期望。
一阶绝对矩是只变量与均值差的绝对值的平均： - 如存在一个 N 维向量 \(u_{1},u_{2}\cdots u_{N}\)
- 则其一阶矩为： \[ \bar{u} = E\left ( u \right ) = \frac{\sum_{N}^{i=0}u}{N} \]
- 其一阶绝对矩为： \[ \left | \bar{u} \right |=\frac{\sum_{N}^{i=0}\left | u_{i} - \bar{u}\right |}{N} \]
- 当一阶矩为 0 时，一阶绝对矩为 1，证明：令N维向量一阶矩为0,一阶绝对矩为1
2.2 对极几何模型
对极几何（Epipolar Geometry）描述了同一场景在两幅图像之间的视觉几何关系；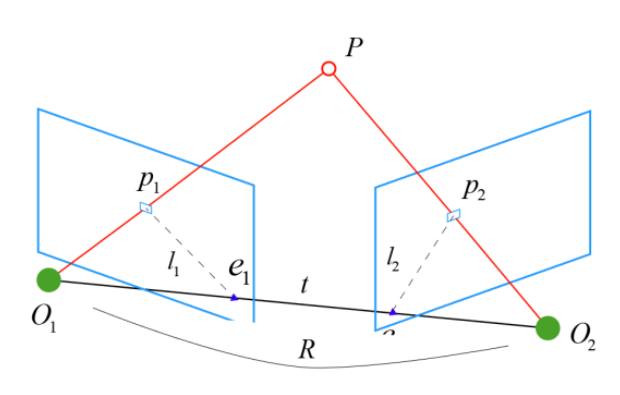
- 假设空间中一个 3D 点 P 在第一帧中的坐标为：\(P=\left [ X,Y,Z \right ]^{T}\)；
- 该点投影到两帧图像中得到像素平面的两个 2D 点 \(p_{1},p_{2}\) ，根据相机模型，其与 3D 点之间存在如下对应关系：
- 其中 K 是相机内参，R,t 是两帧间的相机运动。 \[ s_{1}p_{1}=KP,\quad s_{2}p_{2}=K\left ( RP+t \right )\qquad (1) \]
- 如果使用齐次坐标，也可以将上式写成在乘以非零常数（up to scale）下成立的形式： \[ p_{1}=KP,\quad p_{2}=K\left ( RP+t \right )\qquad (2) \]
- 然后将两点的像素坐标 \(p_{1},p_{2}\) 转换到归一化坐标系 \(x_{1},x_{2}\) 下 \[ x_{1}=K^{-1}p_{1},\qquad x_{2}=K^{-1}p_{2} \qquad(3) \]
- 将公式（3）中的 \(p_{1},p_{2}\) 用公式（2）代替，得到： \[ x_{2}=Rx_{1}+t \qquad(4) \]
- 对公式（4）左右两边同时左乘 \(t^{\wedge }\) 即左右两侧与 \(t\) 做外积 \[ t^{\wedge }x_{2}=t^{\wedge }Rx_{1} \qquad(5) \]
- 再对公式（5）左右两侧同时左乘 \(x_{2}^{T}\) \[ x_{2}^{T}\cdot t^{\wedge }x_{2}=x_{2}^{T}\cdot t^{\wedge }Rx_{1} \qquad(6) \]
- 观察公式（5），\(t^{\wedge }x_{2}\) 是 \(t\) 和 \(x_{2}\) 两个向量的外积，所以其与 \(t\) 和 \(x_{2}\) 均垂直，所以等式左边等于 0，所以公式（5）等价于： \[ x_{2}^{T}\cdot t^{\wedge }R \cdot x_{1}=0 \qquad(7) \]
- 将公式（3）带入到公式（5）中有 \[
p_{2}^{T}K^{-T} \cdot t^{\wedge }R \cdot K^{-1}p_{1} =0 \qquad(8)
\] 上面的公式（8）称之为对极约束，其同时包含了旋转和平移，几何意义是 \(O_{1},p,O_{2}\) 三点共面，将公式中间部分记作本质矩阵 E，也可以转换成基础矩阵 F：
\[ E =t^{\wedge }R, \quad F=K^{-T}EK^{-1}, \quad x_{2}^{T}Ex_{1}=p_{2}^{T}Fp_{1}=0 \qquad(9) \]
2.3 归一化八点法求解基本矩阵
- 由上一节的公式（8）可知基础矩阵可以由下式表示，其中 \(p_{1},p_{2}\) 是两帧中的一对匹配点 \[ p_{2}^{T}Fp_{1}=0 \qquad(10) \]
- 矩阵 F 是一个 3 * 3 的矩阵，由于其也是取决于尺度（up to scale）的，减去一个尺度，也就是只有 8 个自由度，一般把第 9 个量固定为 1，或者求一个 9 量的通解。由于每一对匹配点为公式（10）计算 F 系数提供了一个线性方程，现在 8 个未知量，也就需要 8 组匹配点来估计，这就是八点法。由于八点法只利用了 F 矩阵的线性性质，所以可以在线性代数框架下求解。 > 事实上由于平移和旋转各有 3 个自由度，故 \(t^{\wedge }R\) 共有 6 个自由度，但由于尺度等价性，实际上 F 只有 5 个自由度，也就是说只需要 5 对点即可以求解 F，但是由于 F 的内在性质是非线性性质的，在求解线性方程时会带来问题，所以一般采用八点法。
- 假设点的坐标为 \(p_{1}=(x,y,1)^T,p_{2}=(x',y',1)^T\)，则公式（10）可以写成 \[ \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} f_{11} & f_{12} & f_{13}\\ f_{21} & f_{22} & f_{23}\\ f_{31} & f_{32} & f_{33} \end{bmatrix} \begin{bmatrix} x'\\ y'\\ 1 \end{bmatrix} =0 \qquad(11) \]
- 将上式展开之后有 \[ x'xf_{11}+x'yf_{12}+x'f_{13}+y'xf_{21}+y'yf_{22}+y'f_{23}+xf_{31}+yf_{32}+f_{33}=0 \qquad(12) \]
- 给定 n 对匹配点提供的 n 组线性方程，得到如下方程 \[ A\mathbf f=\begin{bmatrix} x_1'x_1&x_1'y_1&x_1'&y_1'x_1&y_1'y_1&y_1'&x_1&y_1&1\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ x_n'x_n&x_n'y_n&x_n'&y_n'x_n&y_n'y_n&y_n'&x_n&y_n&1 \end{bmatrix}\mathbf f=\mathbf 0 \qquad(13) \]
- 对于上式，如果存在确定（非零）解，则系数矩阵A的秩最多是 8。由于 F 是齐次矩阵，所以如果矩阵 A 的秩为 8，则在差一个尺度因子的情况下解是唯一的，可以直接用线性算法解得。
- 但如果由于点坐标存在噪声则矩阵 A 的秩可能大于8（也就是等于9，由于 A 是 n×9 的矩阵）。这时候就需要求最小二乘解，这里就可以用 SVD 来求解
- f 的解就是系数矩阵 A 最小奇异值对应的奇异向量，也就是 A 奇异值分解后 \(A=UDV^T\) 中矩阵 V 的最后一列适量，这是在解矢量 f 在约束 \(\begin{Vmatrix}\mathbf f\end{Vmatrix}\) 下取 \(\begin{Vmatrix}A\mathbf f\end{Vmatrix}\) 最小的解；
- 以上算法是解基本矩阵的基本方法，称为 8 点算法；
- 但是由于基础矩阵一个重要的特点是奇异性，F 矩阵的秩为 2。如果基础矩阵是非奇异的，那么所计算的对极线将不重合。所以上述算法解得基础矩阵之后会增加一个奇异性约束。
- 最简便的方法就是修正上述算法中求得的矩阵 F，设最终的解为 \(F'\)，另 \(detF'=0\) 下求得 Frobenius 范数（二范数）\(\begin{Vmatrix}F-F'\end{Vmatrix}\) 最小的 \(F'\)。这种方法的实现还是使用了 SVD 分解，若 \(A=UDV^T\)，此时对角矩阵 \(D=diag(r,s,t)\) 满足 \(r\ge s\ge t\) ，则 \(F'=Udiag(r,s,0)V^T\) 最小化范数 \(\begin{Vmatrix}F-F'\end{Vmatrix}\) ，也就是最终的解。
- 所以总结一下八点法的步骤：
- 1. 求线性解： 由系数矩阵 A 最小奇异值对应的奇异矢量 f 求的 F。
- 2. 奇异性约束： 最小化 Frobenius 范数 \(\begin{Vmatrix}F-F'\end{Vmatrix}\) 的 \(F'\) 代替 \(F\) 。
- 这部分来自于许可师兄博客，帮助理解八点法的原理。
- 对于方程（13）的解就是对已知的矩阵 A 进行 SVD 分解 \(A=U\Sigma V^{T}\) 得到的矩阵 V 最右边一列的值 f 并转换成 3 × 3 的初步 F 矩阵。
// 进行第一次奇异值分解,求解出基础矩阵, 使用 cv::SVDecomp() 函数
cv::SVDecomp( A, // 输入，待进行奇异值分解的矩阵.
w, // 输出，奇异值矩阵.
u, // 输出，矩阵 u.
vt, // 输出，矩阵 v 的转置.
cv::SVD::MODIFY_A | //输入，MODIFY_A是指允许计算函数可以修改待分解的矩阵，官方文档上说这样可以加快计算速度、节省内存
cv::SVD::FULL_UV); //FULL_UV=把U和VT补充成单位正交方阵
// 得到 V 的最后一列 9 个量，转换成 3*3 的矩阵.
cv::Mat Fpre = vt.row(8).reshape(0, 3); // v的最后一列- 注意基础矩阵的定义中，由于左乘可一个 \(t^{\wedge }\) ，这个矩阵由于是从三维向量拓展过来的因此他的秩为 2，所以正确的基础矩阵的秩序应当小于等于 2。另外如果这些匹配点都在一个平面上那就会出现 A 的秩小于 8 的情况，这时会出现多解，导致 F 矩阵可能是错误的。所以还需要对上一步初步求解出的 F 矩阵进行处理，由于基础矩阵的秩为 2，而我们不敢保证计算得到的这个结果的秩为2，所以需要通过第二次奇异值分解,来强制使其秩为 2，将奇异值矩阵第三个奇异值设为 0，得到最后的基础矩阵： \[ F'=Udiag(r,s,0)V^T \]
// 对初步得来的基础矩阵继续进行一次奇异值分解
cv::SVDecomp(Fpre, w, u, vt, cv::SVD::MODIFY_A | cv::SVD::FULL_UV);
// 强制将第三个奇异值设置为 0
w.at<float>(2)=0; // 秩2约束，将第3个奇异值设为0
// 重新组合好满足秩约束的基础矩阵，作为最终计算结果返回
return u*cv::Mat::diag(w)*vt;2.4 计算矩阵得分
基础矩阵将点到极限的平方作为误差，计算卡方距离，注意这里有一个自由度，所以显著性检验使用的阈值也是选择的服从自由度为 1 的卡方分布的 0.95 的阈值 3.84。
- 由于基础矩阵的形式 \(x_{2}^{T}Fx_{1}=0\) 使它不能像单应矩阵那样经过求逆直接得到点，但可以得到一条线。
- 假设参考帧 1 上点的坐标为 \([u_1,v_1,1]^{\text{T}}\)，当前帧 2 上匹配的特征点坐标为 \([u_2,v_2,1]^{\text{T}}\)，那么从当前帧到参考帧的重投影将产生一个直线 \(\mathbf{l}_2\)：（也就是在参考帧 1 中相机的极线为 \(\mathbf{l}_2\)，来自于 \(x_{2}^{T}\cdot Fx_{1}=0 \Rightarrow x_{1}^{T}\cdot F^{-1}x_{2}=0\Rightarrow x_{1}^{T}\cdot \mathbf{l}_2 =0\)） \[ \mathbf{l}_2= \begin{bmatrix} a_2\\b_2\\c_2 \end{bmatrix} = \begin{bmatrix} f_1&f_2&f_3\\ f_4&f_5&f_6\\ f_7&f_8&f_9 \end{bmatrix}^{-1} \begin{bmatrix} u_2\\v_2\\1 \end{bmatrix} \]
- 在理想状态下点 \([u_1,v_1,1]^{\text{T}}\) 应该完全在直线 \(\mathbf{l}_2\) 上，这里重投影误差的定义就是：原真实的特征点坐标 \([u_1,v_1,1]^{\text{T}}\) 到根据基础矩阵投影得到的直线 \(\mathbf{l}_2\) 的距离：
- 如果假设距离服从均值为 0，方差为 1 个pixel 的正态分布，那么 \(Delta_{1\leftarrow2} ^2\) 是服从 1 个自由度的 \(\chi ^{2}\) 分布的，因此阈值取的是3.84。 \[ Delta_{1\leftarrow2} ^2= \frac{(a_2u_1+b_2v_1+c_2)^2}{(a_2^2+b_2^2)} \]
- 同时，还需要将误差归一化 \[ e_{1\leftarrow2}^2=\frac{ \Delta_{1\leftarrow2} ^2}{\sigma^2} \]
// l2=F21x1=(a2,b2,c2)
// F21x1可以算出x1在图像中x2对应的线l
// 将参考帧中的特征点以给出的基础矩阵投影到当前帧上，下面的计算完完全全就是矩阵计算的展开
// 注意为了方便计算，这里投影所得到的向量的形式正好是一条2D直线，三个参数对应这直线方程的三个参数
const float a2 = f11*u1+f12*v1+f13;
const float b2 = f21*u1+f22*v1+f23;
const float c2 = f31*u1+f32*v1+f33;
// 理想状态下：x2应该在l这条线上:x2点乘l = 0
// 计算点到直线距离，这里是分子
const float num2 = a2*u2+b2*v2+c2;
// 计算重投影误差，这里的重投影误差其实是这样子定义的
// 注意这里计算的只有一个平方项
const float squareDist1 = num2*num2/(a2*a2+b2*b2); // 点到线的几何距离 的平方
// 归一化误差
const float chiSquare1 = squareDist1*invSigmaSquare;- 然后判断误差是否大于 3.841，如果大于则认为是外点，否则就对其误差进行累加对当前使用的基础矩阵的 RANSAC 评分。
- 同理从参考帧到当前帧也进行一次这样的重投影误差计算，并对误差进行累加。
2.5 从 F 矩阵中恢复相机运动 R, t
从前面计算的基础矩阵中恢复出旋转和平移可以通过对本质矩阵 SVD 奇异值分解实现。 + 首先根据相机内参和基础矩阵计算本质矩阵 E \[ \mathbf{E}=\mathbf{K}^{\text{T}}\mathbf{F}\mathbf{K} \] + 然后对本质矩阵进行奇异值分解 \[ \mathbf{E}=\mathbf{U}\mathbf{\Sigma}\mathbf{V}^{\text{T}} \] + 其中 U，V 是正交矩阵，\(\mathbf{\Sigma}\) 为奇异值矩阵，根据本质矩阵的内在性质，有 \(\mathbf{\Sigma}=diag\left ( \sigma ,\sigma ,0 \right )\) + 令 W 表示沿 Z 轴旋转 90° 得到的旋转矩阵 \[ \mathbf{W}=\mathbf{R}_z(\frac{\pi}{2}) = \begin{bmatrix} 0 & -1& 0\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{bmatrix} \] + 对于任意一个 E，对它分解都能得到两个与之对应的 R 和 t ，所以一共存在 4 组 [R,t] 解 \[ \mathbf{E}=[\mathbf{R}|\mathbf{t}]= \left\{\begin{matrix} \mathbf{R}_1=\mathbf{U}\mathbf{W}\mathbf{V}^{\text{T}}\\ \mathbf{R}_2=\mathbf{U}\mathbf{W}^{\text{T}}\mathbf{V}^{\text{T}}\\ \mathbf{t}_1=\mathbf{U}_3\\ \mathbf{t}_2=-\mathbf{U}_3 \end{matrix}\right. \] + 如何选择正确的 [R,t] ：统计这四个模型中 3D 点在摄像头前方投影误差小于给定阈值的 3D 点个数和每个模型下较大的视差角，如果其中一个模型的视差角大于阈值，并且满足条件的3D点明显大于其他模型,那么这个模型就是最优的选择。
2.6 三角化 3D 点
- 计算第一个相机的投影矩阵 \[
P_{1} = K \ast T_{1}=K \ast \left [ I| 0 \right ]
\]
- 并将第一个相机的光心作为世界坐标系坐标原点 \(O_1\)
- 计算第二个相机的投影矩阵，其中 R，t 来自于前面的矩阵分解 \[
P_{2} = K \ast T_{2}=K \ast \left [ R| t \right ]
\]
- 将第二个相机的光心的位置表示为 \[ \mathbf{O}_2=-R^{T}t \]
- 对于上面公式的解释：在 ORB_SLAM 里，位移向量 \(t_{cw}\) 的方向是从下标左边到右边的，并且位于下标左边坐标系下， \(R_{cw}\) 是从世界坐标系到相机坐标系的旋转， \(R^{T}\) 表示 R 的逆旋转（旋转矩阵是正交矩阵，其转置等于其逆），首先我们把相机系下的 t 变换到世界坐标系下的平移，然后再加一个符号表示世界坐标系到相机坐标系的平移，就是相机光心的位置。
- 假设 3D 点 X（齐次坐标）在两帧下的投影点为 \(x_1, x_2\) ，存在如下对应关系 \[
x_1 = P_1 X, \quad x_2 = P_2 X
\]
- 将其展开并写成齐次坐标形式 \[ \begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \lambda \begin{bmatrix} p1 & p1 & p3 & p4\\ p5 & p6 & p7 & p8\\ p9 & p10 & p11 & p12 \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z\\ 1 \end{bmatrix} \]
- 也可简写成 \[ \begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \lambda \begin{bmatrix} - & P_0 & -\\ - & P_1 & -\\ - & P_2 & - \end{bmatrix} \begin{bmatrix} -\\ X\\ - \end{bmatrix} \]
- 对于上式，展开可以写成 \[
\left\{\begin{matrix}
u = \lambda P_0X\\
v = \lambda P_1X\\
1 = \lambda P_2X
\end{matrix}\right.
\]
- 对第一行等式左右两边均乘以 1（即第三行）得到 \(P_0 - uP_1 = 0\)；
- 对第二行等式左右两边均乘以 1（即第三行）得到 \(vP_2 - P_1= 0\)；
- 对第一行和第二行相互带入，得到 \(uP_1 - vP_0= 0\)。
- 由上面三个等式对一个点可以进行 DLT 求解 \[ \begin{bmatrix} vP_2 - P_1\\ P_0 - uP_1\\ uP_1 - vP_0 \end{bmatrix} X = \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix} \]
- 对于一对匹配点，可以构造一个四元一次正定方程组，求解出 3D 点 X
- 这里的 \(u_1,v_1\) 是第一帧的特征点， \(P_{10}\) 表示第一帧的投影矩阵的第一行 \[ \begin{bmatrix} v_1P_{12} - P_{11}\\ P_{10} - u_1P_{11}\\ v_2P_{22} - P_{21}\\ P_{20} - u_2P_{21} \end{bmatrix} X = \begin{bmatrix} 0\\ 0\\ 0\\ 0 \end{bmatrix} \]
- 在代码中求解时，将 X 前的系数矩阵记作 A，对其进行奇异值分解，分解的结果（X 的 3D 坐标）即矩阵 V 的最后一列（V 的转置的最后一行）
void Initializer::Triangulate( const cv::KeyPoint &kp1, // 特征点, in reference frame const cv::KeyPoint &kp2, // 特征点, in current frame const cv::Mat &P1, // 投影矩阵P1 const cv::Mat &P2, // 投影矩阵P2 cv::Mat &x3D) // 三维点 { cv::Mat A(4,4,CV_32F); //构造参数矩阵A A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0); A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1); A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0); A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1); //奇异值分解的结果 cv::Mat u,w,vt; //对系数矩阵A进行奇异值分解 cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV); //根据前面的结论，奇异值分解右矩阵的最后一行其实就是解，原理类似于前面的求最小二乘解，四个未知数四个方程正好正定 //别忘了我们更习惯用列向量来表示一个点的空间坐标 x3D = vt.row(3).t(); //为了符合齐次坐标的形式，使最后一维为1 x3D = x3D.rowRange(0,3)/x3D.at<float>(3); }
3. Homography 单应矩阵求解变换
4. 全局 BA 优化
【Q】问题
- 第二个相机的光心位置？
- 算法流程中创建初始地图部分有遗漏，待补充。.
- H 矩阵分解待补充。
- 全局 BA 优化放到优化部分中进行。
参考资料
- [1] 吴博师兄 ppt
- [2] 许可师兄博客：基本矩阵的基本解法之8点算法
- [3] 一起学ORBSLAM2（5）ORBSLAM的单目视觉处理方式
- [4] [ORB-SLAM2]单目初始化
- [5] 对极几何
- [6] 本质矩阵
- [7] 万有文：单目SLAM基础知识
- [8] ORB-SLAM2 注释代码
2019.06.17
wuyanminmax@gmail.com